PoliMI Home page
DEIB Home page Fabio Dercole

Generalità

Posizione attuale

Posizioni in visita presso istituti internazionali

Posizioni precedenti

Formazione

Riconoscimenti

Attività scientifica

Attività didattica

Attività editoriale, organizzativa e di servizio

Progetti di ricerca

Presentazione delle pubblicazioni più significative

Pubblicazioni

Generalità

Fabio Dercole
Nato a Milano il 17/11/1974, cittadinanza Italiana
E-mail: fabio.dercole@polimi.it

Inizio pagina

Posizione attuale

Ricercatore universitario di ruolo (dal 3/1/2005), s. s. d. ING-INF/04 – Automatica, presso il Dipartimento di Elettronica e Informazione, Politecnico di Milano.

Inizio pagina

Posizioni in visita presso istituti internazionali

Inizio pagina

Posizioni precedenti

Inizio pagina

Formazione

Inizio pagina

Riconoscimenti


Premi


Borse di studio

Inizio pagina

Attività scientifica

Elenco sintetico delle linee di ricerca più significative:

Analisi di processi di innovazione e competizione

In campi anche molto diversi, come quelli della biologia, della tecnologia dell'informazione e della sociologia, sono facilmente riconoscibili meccanismi di innovazione e competizione. Ciò avviene in sistemi complessi, costituiti da singole entità (individui, microprocessori, autoveicoli, compagnie assicurative, regole semantiche,...) raggruppabili in funzione delle loro caratteristiche, spesso chiamate ``tratti'' (morfologia, potenza di calcolo, cilindrata, premio, strutture sintattiche,...).

Per fissati valori dei tratti, ovvero in assenza di innovazione, la dinamica delle dimensioni dei singoli gruppi è regolata da meccanismi di competizione, e può essere formalizzata con opportuni modelli dinamici non lineari. Un'innovazione consiste nella nascita di un gruppo di poche entità caratterizzate da un valore innovativo di qualche tratto. Ad un evento di innovazione segue un processo di competizione tra il gruppo innovativo e i gruppi preesistenti (residenti) che determina il successo o meno dell'innovazione e quindi la nuova struttura del sistema.

Tenendo conto che le variazioni dei tratti sono decisamente più lente di quelle delle dimensioni dei gruppi è possibile inferire la lenta evoluzione dei tratti caratterizzanti il sistema, in termini di un sistema di equazioni differenziali, tipicamente non lineari, detto equazione canonica della dinamica adatttiva. Infatti, il passo elementare del processo di innovazione si verifica quando il gruppo innovativo sostituisce un gruppo residente. Se invece gruppi innovativi e residenti coesistono nel sistema ha luogo un aumento del numero di gruppi residenti, detto ``branching'', che porta ad un aumento della diversità e della complessità propria del sistema. E' possibile anche il passo contrario, ovvero l'estinzione di gruppi residenti. Infatti, al variare dei tratti, variano anche le dimensioni dei singoli gruppi, che al limite possono annullarsi.

L'analisi e il controllo di processi di innovazione e competizione sono particolarmente complessi in quanto la dinamica dei tratti è descritta da modelli tipicamente non lineari a dimensione variabile, che cresce in seguito a eventi di branching e decresce in seguito a eventi di estinzione. La complessità di tali processi non è quindi solo legata ai tipici fenomeni non lineari come attrattori periodici o caotici, e molteplicità di attrattori, ma anche all'insorgere di attrattori che coinvolgono sequenze periodiche o caotiche di eventi di branching e estinzione. I problemi di analisi e controllo di processi di innovazione e competizione sono pertanto ricondotti all'analisi parametrica dei possibili regimi asintotici (tecnicamente analisi teorica e numerica delle ``biforcazioni'' del sistema), in quanto la conoscenza del quadro qualitativo di tali regimi al variare dei parametri fornisce informazione completa per il controllo parametrico e quindi la per la sintesi di politiche di controllo.

L'attività di ricerca in quest'ambito ha prodotto vari contributi originali, alcuni dei quali raccolti nel libro a diffusione internazionale ``Analysis of Evolutionary Processes: The Adaptive Dynamics Approach and its Applications'', edito da Princeton University Press [LI1].

Contributi metodologici: Contributi applicativi:

Teoria dei giochi evolutiva



Contributi applicativi:

Reti di sistemi dinamici e fenomeni collettivi

Lo studio delle reti composte da sistemi non lineari dinamici è di grande attualità e importanza per due ragioni principali: in primo luogo esse rappresentano un modello adeguato per descrivere la formazione di configurazioni spaziali (pattern) e fenomeni collettivi, quali la sincronizzazione, in numerose discipline (biologia, chimica, ecologia, ingegneria e fisica); inoltre esse simulano la tipica architettura di un computer neurale e pertanto rappresentano modelli biologicamente ispirati per l'elaborazione dell'informazione.

Contributi metodologici: Contributi applicativi:

Analisi di modelli dinamici strutturati

Sistemi dinamici naturali e artificiali con un grado di libertà strutturale, come, ad esempio, spazio, età, taglia, o altri tratti caratteristici sono spesso descritti da equazioni integro-differenziali monodimensionali a derivate parziali. Le soluzioni di equilibrio di tali sistemi descrivono le distribuzioni stazionarie del sistema rispetto al grado di libertà strutturale e sono tecnicamente definite da problemi ai limiti di frontiera per equazioni differenziali ordinarie. Il calcolo e la continuazione nello spazio dei parametri di tali soluzioni e delle loro biforcazioni è pertanto un problema di rilevante importanza sia in fase di analisi che in fase di sintesi di politiche di controllo.

In particolare, molta attenzione è stata recentemente data a distribuzioni stazionarie a ``legge di potenza'', in quanto tali distribuzioni sono state sperimentalmente osservate in molti settori attraverso statistiche di svariati fenomeni, come terremoti, valanghe, incendi forestali e topologia di reti di trasmissione naturali e artificiali. L'analisi delle condizioni di esistenza di distribuzioni stazionarie a legge di potenza e il controllo parametrico di tali condizioni è pertanto un argomento rilevante.

Contributi metodologici: Contributi applicativi:

Analisi di dati e modelli per la bioingegneria



Contributi applicativi:

Analisi di sistemi dinamici discontinui

Numerosi fenomeni fisici sono per loro natura descritti mediante sistemi dinamici discontinui, ovvero sistemi, tipicamente non lineari, in cui le relazioni tra le variabili di stato subiscono delle irregolarità. Lo studio di tali sistemi è intrapreso ormai da qualche decennio e ha generato svariati risultati teorici e soprattuo una folta gamma di applicazioni in vari settori delle scienze e dell'ingegneria. Malgrado ciò sono presenti a tutt'oggi vaste lacune, sia sul piano teorico che sulla messa a punto di efficaci metodi di analisi numerica.

Più specificamente, si considerano sistemi dinamici non lineari di dimensione finita $n$ descritti da equazioni differenziali $\dot{x}=f(x)$ e caratterizzati da discontinuità che si verificano quando lo stato $x$ del sistema raggiunge una varietà $M$ di dimensione $(n-1)$.

Una prima (e forse più nota) classe di sistemi discontinui è quella dei ``sistemi di Filippov'', in cui il campo vettoriale $f$ è discontinuo sulla varietà $M$. In questi sistemi si può avere il caso interessante in cui i due campi vettoriali forzano lo stato del sistema ad attraversare la varietà $M$, così che il risultato è un moto di scivolamento (sliding) sulla varietà. Numerose sono le applicazioni in cui si incontrano sistemi di Filippov, soprattutto nel contesto dell'automazione con regolatori a soglia.

Una seconda classe di sistemi discontinui è quella dei ``sistemi a impatto'', descritti, oltre che dal campo $f$, da una trasformazione $T(x)$ per $x\in M$. In questi sistemi, la traiettoria è la concatenazione di segmenti lenti (descritti dal campo vettoriale $f$) e di segmenti infinitamente veloci (descritti dalla trasformazione $T$).

Una terza classe di sistemi discontinui è invece quella in cui il raggiungimento della varietà $M$ implica la distruzione del sistema stesso. Tali sistemi sono pertanto definiti in un sottoinsieme dello spazio di stato ${\bf R}^n$ limitato dalla varietà $M$. Per garantire la sostenibilità di tali sistemi, pertanto, è essenziale che i suoi attrattori non vengano in contatto, al variare di qualche parametro di controllo, con la varietà $M$.

Nel caso in cui $f$ e/o $M$ dipendano da uno o più parametri $p$ (di progetto o di controllo), è importante poter determinare l'intero catalogo dei modi di funzionamento del sistema al variare di $p$ in un campo preassegnato. Per risolvere questo problema si deve eseguire un'analisi delle biforcazioni del sistema, tenendo conto che la discontinuità su $M$ crea delle biforcazioni del tutto nuove rispetto a quelle note per i sistemi continui.

Contributi metodologici: Contributi applicativi:

Tecniche di continuazione numerica

La continuazione numerica si propone di generare per punti una curva definita implicitamente da un certo numero, diciamo $q$, di equazioni in $q+1$ variabili, $F(y)=0$, $y\in{\mathbf{R}}^{q+1}$, $F:{\mathbf{R}}^{q+1}\to{\mathbf{R}}^{q}$. Per curva si intende pertanto una varietà monodimensionale $y(s)$ in ${\mathbf{R}}^{q+1}$, dove $s\in{\mathbf{R}}$ parametrizza la curva, come per esempio l'ascissa curvilinea misurata a partire da un punto noto $y^0=y(0)$.

I metodi di continuazione fanno tutti riferimento a uno schema ``predictor-corrector'', dove dato un punto $y^i$ sulla curva, il punto successivo $y^{i+1}$ viene calcolato correggendo una predizione iniziale $y^{i+1,0}$ presa lungo la direzione tangente alla curva in $y^i$, ovvero $y^{i+1,0}=y^i+\Delta s\,\phi^i$ con $F_y(y^i)\phi^i=0$, $\phi^{i\scriptscriptstyle \top}\phi^i=1$ ($F_y(y)$ essendo la matrice Jacobiana, $q\times q+1$, di $F(y)$). La fase di correzione si basa su uno dei metodi iterativi per il calcolo di zeri di funzione, tipicamente Newton, applicato alla coppia $F(y)=0$, $\gamma(y)=0$, dove $\gamma:{\mathbf{R}}^{q+1}\to{\mathbf{R}}$ è una condizione aggiuntiva che rende il problema ``quadrato'', cioè con $q+1$ equazioni in $q+1$ variabili.

La continuazione è la base per l'analisi numerica delle biforcazioni di sistemi dinamici. Infatti, con riferimento ai sistemi dinamici a tempo continuo $\dot{x}=f(x,p)$, dove $x(t)\in{\mathbf{R}}^n$ è lo stato del sistema al tempo $t$ e $p$ è un vettore di parametri, gli equilibri $\bar{x}$ del sistema sono definiti implicitamente da $f(\bar{x},p)=0$, ovvero da $n$ equazioni in $n+1$ variabili $\bar{x}$ e $p\in\mathbf{R}$, dove un solo parametro è lasciato variabile. Noto un equilibrio $\bar{x}$ per un assegnato valore del parametro $p$, è quindi possibile continuare l'equilibrio al variare di un parametro.

Più complicata, ma del tutto simile, è la definizione di una soluzione periodica (ciclo) del sistema. Le equazioni sono in parte algebriche (sulle condizioni iniziali e finali della traiettoria), in parte differenziali (quelle che definiscono la traiettoria stessa), e in parte integrali (che impongono vincoli sull'intera traiettoria), e costituiscono quindi un problema integro-differenziale ai limiti di frontiera. Per esempio una soluzione periodica di periodo $T$ è definita dal problema
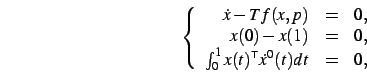
\begin{displaymath} \left\{\begin{array}{rcl} \dot{x}-Tf(x,p) & = & 0,\\ x(0)-x... ...iptscriptstyle \top}\dot{x}^0(t)dt & = & 0, \end{array}\right. \end{displaymath}
dove il vincolo integrale impone che $x(t)$ sia la soluzione periodica più vicina alla soluzione di riferimento $x^0(t)$ (tipicamente l'ultima calcolata durante la continuazione) tra tutte le soluzioni tempo-traslate $x(t-\Delta t)$, $\Delta t\in[0,\,1]$. Più in generale, un problema ai limiti di frontiera si presenta nella forma
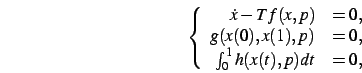
\begin{displaymath} \left\{\begin{array}{rl} \dot{x}-Tf(x,p) &=0,\\ g(x(0),x(1),p) &=0,\\ \int_{0}^{1} h(x(t),p)dt &=0, \end{array}\right. \end{displaymath}
dove $g:\mathbf{R}^n\times\mathbf{R}^n\times\mathbf{R}^{n_p}\to\mathbf{R}^{n_b}$ and $h:\mathbf{R}^n\times\mathbf{R}^{n_p}\to\mathbf{R}^{n_i}$, ovvero $n_b$ è il numero di condizioni al contorno, $n_i$ quello di condizioni integrali e $n_p$ il numero di parametri variabili. Se si vuole che il problema ai limiti di frontiera definisca una curva in $X\times\mathbf{R}^{n_p}$, dove $X$ è un opportuno spazio funzionale per $x(t)$, il numero di parametri variabili deve essere tale da lasciare un solo grado di libertà. Per ciò è utile pensare le $n$ equazioni differenziali come algebriche, $x(1)=\Phi(x(0),T,p)$, e imporre che il numero di variabili, $2n+n_p+1$ se $T$ è variabile, $2n+n_p$ se $T$ è fisso, sia uno in più del numero di equazioni $n+n_b+n_i$. Si ottiene quindi $n_p=n_b+n_i-n$ se $T$ è variabile, e $n_p=n_b+n_i-n+1$ se $T$ è fisso. Considerando $T$ come parametro, si può concludere che $n_p=n_b+n_i-n+1$. Nel caso di una soluzione periodica si ha $n_p=n+1-n+1=2$, cioè è possibile continuare un ciclo con periodo variabile rispetto a un parametro, o un ciclo di periodo assegnato rispetto a due parametri.

I problemi di continuazione si dividono quindi in due categorie: i problemi algebrici e quelli ai limiti di frontiera. Dal punto di vista numerico, i secondi devono necessariamente essere discretizzati, introducendo una griglia temporale, $0=t_0<t_1<\cdots<t_N$, e continuando solo i valori $x(t_i)$, $i=0,\ldots,N$, che sono in numero finito. Di fatto la discretizzazione trasforma il problema ai limiti di frontiera in un grande problema algebrico $F(y)=0$, dove le variabili di continuazione $y$ comprendono tutti i vettori $x(t_i)$ (la dimensione $q$ è quindi di ordine $nN$), oltre che ai parametri, e dove la funzione $F$ è costituita da tutti i vincoli che rendono buona l'approssimazione della soluzione $x(t)$, oltre che dalle condizioni al contorno e da una approssimazione (per quadratura) delle condizioni integrali.

Tornando alle biforcazioni del sistema dinamico, esse possono essere facilmente identificate durante la continuazione di un equilibrio o un ciclo. Per ogni biforcazione è necessario definire una ``funzione test'' che si annulli alla biforcazione e cambi segno, durante la continuazione, a cavallo di essa. Per esempio, il determinante della matrice Jacobiana $f_x(\bar{x},p)$ si annulla quando l'equilibrio $\bar{x}$ non è iperbolico (biforcazione nodo-sella o transcritica). Quando una funzione test $\varphi(y)$ cambia segno tra due successivi punti $y^i$ e $y^{i+1}$, il punto di biforcazione $y^*$ può essere localizzato con la precisione desiderata procedendo opportunamente per bisezione o metodi equivalenti. Inoltre, la condizione $\varphi(y)=0$ può essere aggiunta al problema di continuazione, che quindi richiede un nuovo parametro variabile, diciamo $p_{n_p+1}$, per poter generare, a partire da $(y^*,p_{n_p+1})$, la curva di biforcazione.

Contributi metodologici: Contributi applicativi:

Modelli digitali di territorio

La determinazione della porzione di un territorio visibile da un punto di vista assegnato è un problema rilevante in svariate applicazioni, dall'ottimizzazione di copertura alla grafica compiuterizzata. I più usati algoritmi per il calcolo di visibilità di terreni digitali utilizzano un modello triangolato del territorio, ovvero approssimano la superficie del territorio con una superficie continua costituita da facce triangolari piane i cui vertici sono punti del territorio. Le facce triangolari vengono analizzate in ordine di distanza dal punto di vista, mantenendo aggiornato l'orizzonte definito dalle facce già analizzate. E' infatti l'orizzonte a determinare la parte visibile delle facce adiacenti a quelle già analizzate.

Contributi metodologici:

Inizio pagina

Attività didattica


Attività didattica istituzionale

Incarichi di insegnamento ufficiali

Collaborazione ad attività didattica di insegnamenti ufficiali


Altre attività didattiche

Inizio pagina

Attività editoriale, organizzativa e di servizio


Attività editoriale


Organizzazione di eventi scientifici in sede nazionale ed internazionale


Servizi prestati negli atenei e negli enti di ricerca italiani e stranieri


Partecipazione a commissioni nazionali e internazionale


Affiliazioni e partecipazione a società scientifiche

Inizio pagina

Progetti di ricerca


Coordinamento di progetti di ricerca


Attività in progetti di ricerca nazionali ed internazionali


Partecipazione a bandi di rilevanza internazionale

Inizio pagina

Presentazione delle pubblicazioni più significative

Presentazione del libro

[LI1]

F. Dercole e S. Rinaldi, Analysis of Evolutionary Processes: The Adaptive Dynamics Approach and its Applications, Princeton University Press, Princeton, NJ, 2008.

L'evoluzione per selezione naturale, come detta da Darwin, è certamente il processo dinamico terreno più vecchio, sorprendente e complesso. Ridotto all'essenziale, il cambiamento evolutivo è il risultato due processi di base: innovazione e competizione. L'innovazione altera le caratteristiche ereditarie degli individui, la competizione seleziona le caratteristiche migliori. Le mutazioni genetiche e la competizione per la sopravvivenza giocano questi ruoli negli ecosistemi naturali, ma il paradigma dell'evoluzione Darwiniana va ben oltre e descrive molti sistemi artificiali nelle scienze sociali, economiche e nell'ingegneria.

Gli approcci quantitativi all'evoluzione biologica tradizionalmente considerano il cambiamento evolutivo separatamente dalla demografia delle popolazioni in coevoluzione, la quale però determina la pressione selettiva. Il libro presenta la teoria ``Adaptive Dynamics'' (AD), un approccio modellistico per lo studio di processi di innovazione e competizione che descrive esplicitamente il legame tra cambiamenti demografici e evolutivi. Sacrificando il dettaglio genetico e concentrandosi sull'effetto di innovazioni piccole e rare, AD descrive l'evoluzione mediante un'equazione differenziale ordinaria detta equazione canonica dell'AD. Il numero di popolazioni in coevoluzione può crescere mediante il fenomeno di ``evolutionary branching'', quando le popolazioni innovativa e residente riescono a coesistere, e può ridursi a causa di estinzioni evolutive, una conseguenza controintuitiva dell'evoluzione che può spingere popolazioni in coevoluzione verso l'autodistruzione.

Dopo due capitoli introduttivi (che forniscono rudimenti sui processi evolutivi), la derivazione formale dell'equazione canonica dell'AD è presentata in dettaglio (Capitolo 3), mentre nei sette restanti capitoli varie caratteristiche della dinamica evolutiva sono rivisitate secondo l'approcchio dell'AD. Il contributo principale è quello di mostrare come gli strumenti classici, analitici e numerici, della dinamica non lineare, sistematicamente applicati all'equazione canonica dell'AD, permettano di rispondere efficacemente a domande concettuali di notevole interesse scientifico e culturale.

Altre pubblicazioni correlate: [AI1]–[AI3], [AI6], [AI8], [AI11], [AI14], [AI16], [AI18], [AI20], [AI22].

Presentazione dei 15 articoli più significativi

[AI27]

F. Dercole, M. De Carli, F. Della Rossa e A. V. Papadopoulos, Overpunishing is not necessary to fix cooperation in voluntary public goods games, Journal of Theoretical Biology (accettato per pubblicazione).

L'emergere e il mantenimento di comportamenti cooperativi in comunità (animali o umane) di individui senza legami di amicizia o parentela è uno dei problemi fondamentali e più controversi delle scienze biologiche e sociali. E' tipicamente studiato attraverso i cosiddetti ``public goods games'', la generalizzazione del dilemma del prigioniero a gruppi con più di due individui interagenti. Studi sia sperimentali che teorici hanno mostrato come la combinazione della partecipazione volontaria e della punizione altruistica dei comportamenti anti-sociali, ovvero punizioni inflitte volontariamente e sostenendone il costo da contribuenti al ``public good'' verso sfuttatori non contribuenti, favorisce l'instaurarsi di regimi di cooperazione diffusa. Il meccanismo di punizione usato in tali studi è però particolarmente severo, perchè ogni individuo sfruttatore riceve una sanzione da ognuno dei punitori presenti nel gruppo che ha partecipato al gioco. In questo studio, un meccanismo di punizione più debole e meno costoso, nel quale lo sfruttatore riceve al più una sanzione fissa e dove i relativi costi sono divisi tra i punitori presenti, è stato introdotto nell'ambito del più noto e discusso modello di ``public goods game''. L'analisi del modello ha mostrato come risultati analoghi a quelli ottenuti con ``sovrapunizione'', in termini di diffusione della cooperazione, si possono ottenere con il meccanismo proposto.

[AI25]

F. Dercole e F. Della Rossa, Generalized boundary equilibria in n-dimensional Filippov systems: The transition between persistence and nonsmooth-fold scenarios, Physica D, 241, 1903–1910, 2012.

L'articolo analizza una biforcazione di codimensione due (due criticità coinvolte) che coinvolge le soluzioni stazionarie dei sistemi di Filippov (sistemi a tempo continuo definiti da campi vettoriali discontinui; si veda la relativa linea di ricerca). Specificatamente, quando al variare di un parametro del modello un equilibrio iperbolico di uno dei campi vettoriali definenti il sistema collide con una superficie di discontinuità, due scenari possono genericamente presentarsi: la ``persistenza'' della soluzione stazionaria, che passa da tipo ``standard'' a tipo ``pseudo'', ovvero un equilibrio della dinamica di ``sliding'' sulla superficie di discontinuità; la biforcazione ``nonsmooth-fold'', attraverso la quale la soluzione standard collide e sparisce assieme ad una di tipo pseudo. La biforcazione analizzata, detta di equilibrio di bordo generalizzato, è quella in cui oltre ad avere un equilibrio sul bordo, il sistema presenta il cambio di scenario. Mediante la definizione e l'analisi di una opportuna forma canonica, alla quale ricondurre qualsiasi sistema di Filippov che presenti la biforcazione, sono state identificate tutte le soluzioni stazionarie presenti nel sistema localmente alla biforcazione. La teoria presentata è affiancata da un esempio di gestione dello sfruttamento di una risorsa ittica.

Altre pubblicazioni correlate: [CI9].

[AI20]

F. Dercole, R. Ferrière e S. Rinaldi, Chaotic Red Queen coevolution in three-species food chains, Proceedings of the Royal Society of London B, 277, 2321–2330, 2010.

L'articolo presenta il primo esempio di attrattore evoluzionistico caotico e pertanto da una risposta formale positiva al quesito sulla capacità dei meccanismi evolutivi di generare forme di vita sempre innovative, anche a fronte di condizioni ambientali invarianti. Ciò non è sorprendente in se, dato che attrattori caotici sono da tempo ben noti in vari settori delle scienze dove i processi dinamici in gioco sono decisamente più semplici dell'evoluzione. La portata di questo lavoro è pertanto concettuale. Vista l'impossibilità di una verifica sperimentale, che richiederebbe esperimenti o serie temporali su scala di tempo geologica, e dove sarebbe comunque difficile distinguere tra caoticità endogena, generata dai meccanismi di innovazione e competizione alla base dell'evoluzione, e caoticità esogena, attribuibile per esempio ai cambiamenti climatici intercorsi, la risposta non può che arrivare per via modellistica. Inoltre, perchè la risposta sia il più possibile conservativa, e quindi più significativa, il modello deve essere il più semplice possibile, in quanto dettagli aggiuntivi, quali la struttura di età, di taglia e fisiologica delle popolazioni o la descrizione congiunta di più caratteristiche in evoluzione (fenotipi) per popolazione, aumenterebbero la complessità del modello e delle sue soluzioni. Si è quindi considerata la più tipica e semplice delle catene alimentari risorsa-consumatore-predatore caratterizzando ciascuna popolazione con un solo fenotipo. Il modello evolutivo, che descrive la dinamica dei tre fenotipi, è stato ricavato mediante la teoria della ``Adaptive Dynamics'' (si veda [LI1]) e la sua analisi al variare delle frequenze di mutazione (innovazione) ha evidenziato la presenza di attrattori caotici.

Altre pubblicazioni correlate: [LI1], [AI22].

[AI19]

A. Colombo e F. Dercole, Discontinuity induced bifurcations of non-hyperbolic cycles in nonsmooth systems, SIAM Journal on Applied Dynamical Systems, 9, 62–83, 2010.

L'articolo analizza tre biforcazioni di codimensione due (due criticità coinvolte) che coinvolgono soluzioni periodiche di sistemi caratterizzati da qualche tipo di discontinuità al raggiungimento di particolari superfici nello spazio delle variabili di stato (per es. sistemi di Filippov, a impatto, o con spazio di stato delimitato; si veda la relativa linea di ricerca). Analizza in particolare la collisione tangente di un ciclo con una superficie di discontinuità, al variare di due parametri lungo una curva di biforcazione (di codimensione uno) lungo la quale il ciclo risulta non iperbolico (biforcazione nodo-sella, raddoppio di periodo, toro). Tre modelli canonici, ai quali ricondurre qualsiasi sistema di Filippov che presenti una delle tre biforcazioni, sono stati identificati e analizzati, e per ciascun caso è stato discusso un esempio applicativo (rispettivamente: un modello a impatto di incendi forestali, un modello discontinuo di alternanza politica, un modello per l'analisi delle oscillazioni laterali di un treno).

Altre pubblicazioni correlate: [CI4], [AI7].

[AI17]

F. Dercole, BPcont: An Auto driver for the continuation of branch points of algebraic and boundary-value problems, SIAM Journal on Scientific Computing, 30, 2405–2426, 2008.

BPCONT è un software numerico per la continuazione delle biforcazioni transcritiche (``branch points'', BP) sia di problemi algebrici che differenziali (ordinari) ai limiti di frontiera. BPCONT si appoggia su AUTO, il pacchetto software di continuazione numerica più diffuso in ambiente scientifico, ed è disponibile in due versioni: come ``driver'' esterno per AUTO97 e come funzionalità interna delle nuove versioni di AUTO07P. I BP semplici sono punti nello spazio di continuazione dove due famiglie monodimensionali di soluzioni si intersecano trasversalmente. La localizzazione accurata dei BP durante la continuazione di una famiglia di soluzioni e il passaggio alla continuazione della famiglia intersecante sono implementati in AUTO, così come in altri software, ma la continuazione dei BP al variare di ulteriori parametri del problema non è ancora del tutto supportata. BPCONT ne completa il supporto, considerando sia problemi generici, dove la continuazione dei BP richiede di variare due parametri ulteriori, che casi non generici, dove un solo parametro ulteriore è tipicamente sufficiente a causa di simmetrie specifiche del problema. L'articolo presenta i problemi di continuazione, algebrici e differenziali, che definiscono la continuazione dei BP, discute la loro inizializzazione e la tecnica di ``rottura di simmetria'' utilizzata per gestire automaticamente i casi non generici, e descrive l'implementazione di BPCONT. Vari esempi applicativi sono considerati, tra cui problemi algebrici generici e non, problemi differenziali periodici generici e non e un problema differenziale non periodico non generico.

Altre pubblicazioni correlate: [SS2], [SS3].

[AI16]

F. Dercole, U. Dieckmann, M. Obersteiner e S. Rinaldi, Adaptive dynamics and technological change, Technovation, 28, 335–348, 2008.

L'articolo presenta un approccio modellistico all'insorgenza di varietà tecnologica conseguente all'interazione tra dinamiche di mercato e innovazione tecnologica. La competizione tra prodotti esistenti nel mercato e prodotti innovativi genera una evoluzione continua delle caratteristiche tecnologiche dei prodotti di successo, che tipicamente avviene su una scala di tempi più lunga riepetto a quella di pura competizione. Quando l'evoluzione tecnologica raggiunge un equilibrio, questo può essere di tipo ESS (Evolutionarily Stable Strategy), dove le innovazioni marginali non riescono a penetrare il mercato, o di tipo ``branching'', dove i prodotti innovativi coesistono con quelli già affermati (si veda la prima linea di ricerca). Il ``branching'' tecnologico è quindi l'origine della varietà di prodotto. L'articolo principalmente riformula la teoria della ``Adaptive Dynamics'' (AD), recentemente proposta per l'analisi dei processi evolutivi (si veda [LI1]), in contesto economico. Separando le scale di tempo tipiche della competizione di mercato e dei processi d'innovazione, l'AD permette una descrizione formale della coevoluzione tecnologica attraverso equazioni differenziali ordinarie, una per ogni caratteristica in evoluzione. L'articolo inoltre presenta e discute la prima applicazione dell'AD in economia. Il problema considerato è intenzionalmente molto semplice, in modo da mettere in luce chiaramente tutti i passi formali dell'analisi, ma permette di trarre le seguenti conclusioni intuitive: la varietà di prodotto è attesa in settori di mercato caratterizzati da ampia capacità di assorbire tecnologie diverse e che garantiscano nicchie di mercato anche a tecnologie relativamente simili. Le limitazioni dell'approccio AD in economia, così come le direzioni future promettenti in economia e nelle scienze sociali, sono discusse in conclusione.

Altre pubblicazioni correlate: [LI1], [RI4].

[AI15]

A. Colombo, F. Dercole e S. Rinaldi, Remarks on metacommunities synchronization with application to prey-predator systems, The American Naturalist, 171, 430–442, 2008.

Le spiegazioni comunemente fornite in letteratura per i fenomeni di sincronizzazione in metapopolazioni si possono riunire in due gruppi: uno attribuisce gli effetti di sincronizzazione alla presenza di una forzante globale, che agisce in modo simile su tutti i sistemi in rete (sincronizzazione per cause esogene), l'altro spiega l'emergere di sincronizzazione per effetto dell'accoppiamento tra i sistemi in rete (sincronizzazione per cause endogene), che in termini ecologici corrisponde a flussi migratori tra i vari compartimenti (celle). Al fine di sviluppare un modello che tenga conto delle diverse cause di sincronizzazione, e di studiarne gli effetti combinati, una generica metapopolazione è stata descritta da una rete di sistemi dinamici a tempo continuo opportunamente interconnessi, ciascuno influenzato da una forzante (metereologica) globale generata da un oscillatore autonomo caotico. Questo approccio si differenzia radicalmente dai metodi tradizionalmente usati in questo contesto, sostanzialmente basati su analisi statistiche di correlazione tra compartimenti. Cio' ha permesso di inquadrare il problema nell'ambito della teoria delle reti di sistemi dinamici, e di estendere noti risultati di sincronizzazione al caso di presenza di forzante globale. Il risultato principale consiste nella derivazione della condizione di sincronizzazione per cause esogene, ovvero in assenza di flussi migratori, nel caso particolare di celle identiche. Tale condizione dipende solamente dalla dinamica della singola cella forzata e garantisce la sincronizzazione della rete quando la cella non aggiunge caoticità a quella metereologica (assenza di ``biocaos''). In termini tecnici ciò corrisponde ad avere esponenti di Lyapunov negativi nella singola cella condizionata dalla metereologia. Quando la condizione non è verificata, la sincronizzazione per cause miste (esogene e endogene) è garantita da condizioni che estendono semplicemente il noto risultato di sincronizzazione per cause endogene. Tali condizioni coinvolgono un numero di opportuni esponenti di Lyapunov pari al numero di celle nella rete. L'articolo presenta lo studio (numerico) della più classica delle metapopolazioni, composta da catene alimentari preda-predatore. Oltre a verificare le condizioni derivate, lo studio ne mette in evidenza una certa robustezza rispetto a disomogeneità metereologiche e biologiche tra le celle, e discute l'effetto di vari fattori ecologico-ambientali.

Altre pubblicazioni correlate: [AI14].

[AI14]

F. Dercole, D. Loiacono e S. Rinaldi, Synchronization in population networks: A byproduct of darwinian evolution?, International Journal of Bifurcation and Chaos, 7, 2435–2446, 2007.

Le dinamiche collettive svolgono un ruolo centrale in molti fenomeni biologici e sociali. Un esempio di particolare interesse è l'insorgere di dinamiche sincronizzate in ecosistemi spazialmente distribuiti per mezzo di meccanismi diffusivi. Finora queste dinamiche sono state principalmente studiate in assenza di variazioni evolutive dei parametri demografici dell'ecosistema o solo in scenari evolutivi molto particolari. In questo lavoro proponiamo un metodo di analisi più generale che permette di studiare l'emergere della sincronizzazione in reti di ecosistemi caratterizzati da tratti in evoluzione che influenzano diversi parametri demografici. Questo metodo è applicato al caso di due ecosistemi identici di tipo preda-predatore-superpredatore accoppiati. I risultati ottenuti in questo semplice esempio confermano la congettura che l'evoluzione naturale porti le reti di ecosistemi verso debole forme di sincronizzazione.

Altre pubblicazioni correlate: [LI1], [AI15].

[AI13]

F. Dercole, A. Gragnani e S. Rinaldi, Bifurcation analysis of piecewise smooth ecological models, Theoretical Population Biology, 72, 197–213, 2007.

In questo lavoro sono stati analizzati i comportamenti dinamici di catene alimentari descritte mediante modelli dinamici discontinui (in particolare sistemi di Filippov, si veda la corrispondente linea di ricerca). Modelli di questo tipo sono spesso usati per rappresentare popolazioni che scelgono in modo selettivo tra habitat o diete alternative o per descrivere l'evoluzione di una risorsa che viene sfruttata solo se sufficientemente abbondante. Lo studio è stato effettuato mediante l'analisi di biforcazione di opportuni modelli discontinui rispetto a due parametri di controllo. A tale scopo, è stato proposto un metodo di analisi relativamente semplice che permette di costruire passo passo il diagramma di biforcazione completo. Tale metodo è presentato attraverso quattro esempi che riguardano lo sfruttamento, la protezione e la gestione di risorse naturali.

Altre pubblicazioni correlate: [AI4], [AI7], [RI3], [SS1].

[AI11]

F. Dercole, A. Gragnani, R. Ferrière e S. Rinaldi, Coevolution of slow-fast populations: evolutionary sliding, evolutionary pseudo-equilibria and complex Red Queen dynamics, Proceedings of the Royal Society of London B, 273, 983–990, 2006.

L'articolo studia la coevoluzione di due tratti caratterizzanti un sistema risorsa-consumatore che possono coesistere in modo stazionario o periodico a seconda del valore dei tratti (si veda la prima linea di ricerca). La derivazione in forma chiusa della dinamica dei tratti è in pratica impossibile ogni qual volta i gruppi residenti nel sistema coesistono in modo ciclico, in quanto richiederebbe la conoscenza analitica del ciclo limite. Nel caso particolare preso in analisi, la risorsa è caratterizzata da una dinamica molto più rapida di quella del consumatore e pertanto l'attrattore periodico sui cui coesistono risorsa e consumatore è ben approssimato dal così detto ciclo singolare ricavabile in forma chiusa dai risultati classici della teoria delle perturbazioni singolari. Tale ciclo ha ampiezza finita anche per valori dei tratti vicinissimi alla transizione tra equilibrio e ciclo (biforcazione di Hopf), per cui le dinamiche dei tratti nelle regioni separate da tale transizione possono essere anche radicalmente diverse. Il modello risulta pertanto discontinuo e, in particolare, appartenente alla classe dei sistemi di Filippov (si veda la corrispondente linea di ricerca). Il contributo dell'articolo è duplice. In primo luogo descrive, seppur in un caso particolare, un modello di dinamica adattativa di due gruppi interagenti che coesistono in modo ciclico. In secondo luogo applica i risultati di analisi delle biforcazioni di sistemi di Filippov per dedurre svariati scenari adattativi, alcuni dei quali di particolare rilevanza per il controllo e la conservazione degli ecosistemi.

Altre pubblicazioni correlate: [LI1], [AI7], [RI3], [SS1].

[AI7]

F. Dercole e Yu. A. Kuznetsov, SlideCont: An Auto97 driver for bifurcation analysis of Filippov systems, ACM Transactions on Mathematical Software, 31, 95–119, 2005.

SLIDECONT è un software numerico per l'analisi delle biforcazioni sliding di sistemi di Filippov (si veda la linea di ricerca sui sistemi discontinui). SLIDECONT si appoggia su AUTO97, il pacchetto software di continuazione numerica più diffuso in ambiente scientifico. Le biforcazioni sliding sono quelle che coinvolgono qualche moto di scivolamento sulla varietà di discontinuità che caratterizza il sistema. SLIDECONT permette di continuare soluzioni sliding rispetto a un parametro di controllo, di localizzare eventuali biforcazioni di codimensione 1, e di continuarle rispetto a due parametri. Durante tale continuazione, varie biforcazioni di codimensione 2 possono essere localizzate. Tulle le biforcazioni sliding di codimensione 1 di sistemi del secondo ordine sono implementate, e alcune biforcazioni sliding di codimensione 1 e 2 sono implementate per sistemi di qualsiasi ordine. L'articolo descrive la struttura e le capacità di SLIDECONT e presenta tre applicazioni, due sistemi meccanici e uno di controllo.

Altre pubblicazioni correlate: [CI2], [RI3], [SS1].

[AI6]

F. Dercole, Remarks on branching-extinction evolutionary cycles, Journal of Mathematical Biology, 47, 569–580, 2003.

L'articolo mostra come sia possibile che si instauri in una popolazione un regime evolutivo periodico in cui il numero di tratti coesistenti, e quindi la dimensione del sistema, cambiano periodicamente (si veda la prima linea di ricerca). Il problema biologico trattato è quello dell'evoluzione dell'attitudine al cannibalismo, che studi empirici indicano avere una forte componente genetica. Attraverso un modello evolutivo e l'analisi sistematica delle sue biforcazioni viene mostrato come una popolazione possa evolvere verso una alta attitudine al cannibalismo alla quale può coesistere con una popolazione di mutanti leggermente meno cannibalisti (branching). A questo punto, due popolazioni caratterizzate da attitudini cannibaliste diverse, anche se inizialmente molto simili, coevolvono, ma la loro coevoluzione è interrotta dall'estinzione della popolazione più cannibalista, che lascia la rimanente popolazione nuovamente nelle condizioni di evolvere verso un alto livello di cannibalismo. L'identificazione, la continuazione nello spazio dei parametri e l'analisi delle biforcazioni di attrattori evolutivi coinvolgenti eventi di branching e estinzione esula dall'analisi tradizionale dei sistemi dinamici non lineari e richiede lo sviluppo di tecniche ad hoc.

Altre pubblicazioni correlate: [LI1], [AI2].

[AI4]

F. Dercole, A. Gragnani, Yu. A. Kuznetsov e S. Rinaldi, Numerical sliding bifurcation analysis: An application to a relay control system, IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 50, 1058–1063, 2003.

L'articolo affrontata il problema dello sfruttamento delle risorse naturali protette, risorse cioè che non possono essere sfruttate se troppo scarse. Il modello che ne deriva è un modello di controllo composto da un sistema SISO e un controllore on-off. Lo studio dei possibili comportamenti è condotto mediante l'analisi delle biforcazioni sliding del sistema (si veda la linea di ricerca sui sistemi discontinui) al variare dei due parametri di controllo: la soglia di protezione sull'abbondanza della risorsa e l'intensità di sfruttamento. L'analisi mostra come la politica di controllo adottata effettivamente prevenga l'estinzione della risorsa. Per opportune combinazioni dei parametri il sistema protetto presenta però comportamenti stabili alternativi (equilibri e/o cicli, con o senza soluzioni di scivolamento).

Altre pubblicazioni correlate: [CI1], [RI2], [RI3], [SS1].

[AI3]

F. Dercole, J.-O. Irisson e S. Rinaldi, Bifurcation analysis of a prey-predator coevolution model, SIAM Journal on Applied Mathematics, 63, 1378–1391, 2003.

L'articolo discute l'evoluzione di sistemi risorse-consumatori (si veda la prima linea di ricerca). Un tema classico in questo contesto è quello della coevoluzione di popolazioni interagenti di prede e predatori. Il modello in cui per la prima volta regimi evolutivi ciclici (denominati regimi di tipo ``Red Queen'') sono stati osservati, viene esteso e studiato in dettaglio attraverso l'analisi numerica delle sue biforcazioni. I risultanti diagrammi di biforcazione rispetto a varie coppie di parametri ambientali e di controllo mostrano come il catalogo dei comportamenti dinamici dei sistemi in evoluzione possa essere estremamente ricco. Biforcazioni sia locali che globali, opportunamente organizzate attorno a punti strategici di codimensione 2, delimitano regioni dello spazio dei parametri caratterizzate da attrattori multipli, sia stazionari che periodici, da equilibri evolutivi di tipo ``branching'', favorendo la diversificazione della risorsa, e dalla possibile estinzione evolutiva del consumatore.

Altre pubblicazioni correlate: [LI1], [AI11], [CLI5].

[AI1]

F. Dercole, R. Ferrière e S. Rinaldi, Ecological bistability and evolutionary reversals under asymmetrical competition, Evolution, 56, 1081–1090, 2002.

L'articolo dimostra che la coevoluzione, ovvero l'evoluzione di almeno due tratti mutuamente interagenti, non è, come generalmente ritenuto, condizione necessaria per il verificarsi di regimi evolutivi periodici (si veda la prima linea di ricerca). Recenti studi mostrano che stati stabili alternativi, associati a differenti densità di popolazione, possono caratterizzare i sistemi naturali. Questi stati alternativi sono facilmente soggetti a pressioni selettive diverse, che danno luogo a dinamiche adattative diverse a seconda dello stato in cui si trova la popolazione. Cicli evolutivi di un singolo tratto possono pertanto instaurarsi se esistono valori del tratto vicino ai quali tratti innovativi invadono inizialmente ma falliscono nel persistere, mentre la loro presenza temporanea provoca il cambio di stato del tratto residente.

Altre pubblicazioni correlate: [LI1].

Inizio pagina

Pubblicazioni

Libri a diffusione internazionale

[LI1]

F. Dercole e S. Rinaldi, Analysis of Evolutionary Processes: The Adaptive Dynamics Approach and its Applications, Princeton University Press, Princeton, NJ, 2008.

Articoli su riviste internazionali

[AI29]

P. Landi, F. Dercole e S. Rinaldi, Branching Scenarios in eco-evolutionary prey-predator models, SIAM Journal on Applied Mathematics, 73, 1634–1658, 2013.
[AI28]

F. Della Rossa, F. Dercole e C. Piccardi, Profiling core-periphery network structure by random walkers, Scientific Reports, 3, 1467, 2013.
[AI27]

F. Dercole, M. De Carli, F. Della Rossa e A. V. Papadopoulos, Overpunishing is not necessary to fix cooperation in voluntary public goods games, Journal of Theoretical Biology, 326, 70–81, 2013.
[AI26]

M. Barbieri, A. M. Bianchi, S. Cerutti e F. Dercole, Modeling focal and multi-focal epilepsy as a qualitative resonance in networks of chaotic oscillators, International Journal of Bioelectromagnetism, 14, 172–178, 2012.
[AI25]

F. Dercole e F. Della Rossa, Generalized boundary equilibria in n-dimensional Filippov systems: The transition between persistence and nonsmooth-fold scenarios, Physica D, 241, 1903–1910, 2012.
[AI24]

F. Dercole, F. Della Rossa, A. Colombo e Yu. A. Kuznetsov, Two Degenerate Bounday Equilibrium Bifurcations in Planar Filippov Systems, SIAM Journal on Applied Dynamical Systems, 10, 1525–1553, 2011.
[AI23]

S. Cerutti, G. Baselli, A. M. Bianchi, E. Caiani, D. Contini, R. Cubeddu, F. Dercole, L. Di Rienzo, D. Liberati, L. Mainardi, P. Ravazzani, S. Rinaldi, M. G. Signorini e A. Torricelli, Biomedical signal and image processing, IEEE PULSE, 2, 41–54, 2011.
[AI22]

F. Dercole e S. Rinaldi, Evolutionary dynamics can be chaotic: A first example, International Journal of Bifurcation and Chaos, 20, 3473–3485, 2010.
[AI21]

S. Rinaldi, F. Della Rossa e F. Dercole Love and appeal in standard couples, International Journal of Bifurcation and Chaos, 20, 2443–2451, 2010.
[AI20]

F. Dercole, R. Ferrière e S. Rinaldi, Chaotic Red Queen coevolution in three-species food chains, Proceedings of the Royal Society of London B, 277, 2321–2330, 2010.
[AI19]

A. Colombo e F. Dercole, Discontinuity induced bifurcations of non-hyperbolic cycles in nonsmooth systems, SIAM Journal on Applied Dynamical Systems, 9, 62–83, 2010.
[AI18]

F. Dercole, C. Prieu e S. Rinaldi, Technological change and fisheries sustainability: The point of view of Adaptive Dynamics, Ecological Modelling, 221, 379–387, 2010.
[AI17]

F. Dercole, BPcont: An Auto driver for the continuation of branch points of algebraic and boundary-value problems, SIAM Journal on Scientific Computing, 30, 2405–2426, 2008.
[AI16]

F. Dercole, U. Dieckmann, M. Obersteiner e S. Rinaldi, Adaptive dynamics and technological change, Technovation, 28, 335–348, 2008.
[AI15]

A. Colombo, F. Dercole e S. Rinaldi, Remarks on metacommunities synchronization with application to prey-predator systems, The American Naturalist, 171, 430–442, 2008.
[AI14]

F. Dercole, D. Loiacono e S. Rinaldi, Synchronization in population networks: A byproduct of darwinian evolution?, International Journal of Bifurcation and Chaos, 7, 2435–2446, 2007.
[AI13]

F. Dercole, A. Gragnani e S. Rinaldi, Bifurcation analysis of piecewise smooth ecological models, Theoretical Population Biology, 72, 197–213, 2007.
[AI12]

F. Dercole, Self-organized power-law equilibrium distributions in structured dynamical systems, Chaos and Complexity Letters, 2, 113–120, 2006.
[AI11]

F. Dercole, A. Gragnani, R. Ferrière e S. Rinaldi, Coevolution of slow-fast populations: evolutionary sliding, evolutionary pseudo-equilibria and complex Red Queen dynamics, Proceedings of the Royal Society of London B, 273, 983–990, 2005.
[AI10]

F. Dercole e S. Maggi, Detection and continuation of a border collision bifurcation in a forest fire model, Applied Mathematics and Computation, 168, 623–635, 2005.
[AI9]

F. Dercole, K. Niklas e R. Rand, Self-thinning and community persistence in a simple size-structured dynamical model of plant growth, Journal of Mathematical Biology, 51, 333–354, 2005.
[AI8]

F. Dercole, Border collision bifurcations in the evolution of mutualistic interactions, International Journal of Bifurcation and Chaos, 15, 2179–2190, 2005.
[AI7]

F. Dercole e Yu. A. Kuznetsov, SlideCont: An Auto97 driver for bifurcation analysis of Filippov systems, ACM Transactions on Mathematical Software, 31, 95–119, 2005.
[AI6]

F. Dercole, Remarks on branching-extinction evolutionary cycles, Journal of Mathematical Biology, 47, 569–580, 2003.
[AI5]

F. Dercole, Remarks on the computation of the horizon of a digital terrain, Applied Mathematics and Computation, 146, 627–641, 2003.
[AI4]

F. Dercole, A. Gragnani, Yu. A. Kuznetsov e S. Rinaldi, Numerical sliding bifurcation analysis: An application to a relay control system, IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 50, 1058–1063, 2003.
[AI3]

F. Dercole, J.-O. Irisson e S. Rinaldi, Bifurcation analysis of a prey-predator coevolution model, SIAM Journal on Applied Mathematics, 63, 1378–1391, 2003.
[AI2]

F. Dercole e S. Rinaldi, Evolution of cannibalism: Scenarios derived from adaptive dynamics, Theoretical Population Biology, 62, 365–374, 2002.
[AI1]

F. Dercole, R. Ferrière e S. Rinaldi, Ecological bistability and evolutionary reversals under asymmetrical competition, Evolution, 56, 1081–1090, 2002.

Capitoli di libri a diffusione internazionale

[CLI5]

F. Dercole e S. Rinaldi, Bifurcation analysis of the adaptive dynamics canonical equation, in Elements of Adaptive Dynamics, J. A. J. Metz e U. Dieckmann (eds.), Cambridge University Press, Cambridge UK (di prossima pubblicazione).
[CLI4]

F. Dercole e S. Rinaldi, Bifurcations, in Encyclopedia of Theoretical Ecology, A. Hastings and L. Gross (eds.), pp.88–95, University of California Press, Berkeley, CA, 2012.
[CLI3]

F. Dercole e S. Rinaldi, Dynamical Systems and Their Bifurcations, in Advanced Methods of Biomedical Signal Processing, S. Cerutti and C. Marchesi (eds.), pp.291–325, IEEE-Wiley Press, New York, NY, 2011.
[CLI2]

H. G. E. Meijer, F. Dercole e B. E. Oldeman, Numerical Bifurcation Analysis, in Encyclopedia of Complexity and System Science, Robert A. Meyers (ed.), pp.6329–6352, Springer-Verlag, Berlin, 2009.
[CLI1]

A. Lazaric, E. Munoz de Cote, F. Dercole e M. Restelli, Bifurcation Analysis of Reinforcement Learning Agents, in Adaptive Agents and Multi-Agent Systems III, K. Tuyls, A. Nowe, Z. Guessoum, and D. Kudenko (eds.), Lecture Notes in Artificial Intelligence, vol. 4865, pp.129–144, Springer-Verlag, Berlin, 2008.

Comunicazioni a congressi, simposi, workshops internazionali

FD ha partecipato a svariati congressi internazionali che non prevedono atti stampati, come congressi SIAM (Society for Industrial and Applied Mathematics) e ESMTB (European Society for Mathematical and Theoretical Biology).

[CI16]

P. Landi e F. Dercole, The evolution of fashion traits: Pure social interactions promote diversity, in Proceedings of the 8th European Nonlinear Dynamics Conference, ENOC2014, Vienna, 2014.
[CI15]

F. Della Rossa e F. Dercole, Automatic system perturbation for the continuation of codim-1 transcritical bifurcations in MatCont, in Proceedings of the 8th European Nonlinear Dynamics Conference, ENOC2014, Vienna, 2014.
[CI14]

F. Della Rossa, F. Dercole e M. Lovera Chaotic dynamics in an Earth pointing, magnetically controlled spacecraft, in Proceedings of the 8th European Nonlinear Dynamics Conference, ENOC2014, Vienna, 2014.
[CI13]

F. Della Rossa, F. Dercole e M. Lovera, Attitude stability analysis for an Earth pointing, magnetically controlled spacecraft, in Proceedings of the 19th IFAC Symposium on Automatic Control in Aerospace, ACA 2013, pp. 508–513, Würzburg, Germany, 2013.
[CI12]

F. Della Rossa e F. Dercole, Generic and generalized boundary operating points in piecewise-linear (discontinuous) control systems, in Proceedings of the 51st IEEE Conference on Decision and Control, CDC 2012, Maui, Hawaii, 2012.
[CI11]

M. Barbieri, A. M. Bianchi, S. Cerutti e F. Dercole, Qualitative resonance in networks of chaotic oscillators: A modeling framework for focal and multi-focal epilepsy, in Proceedings of the 7th International Workshop on Biosignal Interpretation, BSI2012, pp. 205–208, Como, 2012.
[CI10]

F. Dercole, F. Della Rossa, A. Colombo e Yu. A. Kuznetsov, Codimension-two singularities on the stability boundary in 2D Filippov systems, in Proceedings of the 18th IFAC World Congress, pp. 13281–13286, Milano, 2011.
[CI9]

F. Della Rossa e F. Dercole, The Transition from Persistence to Nonsmooth-Fold Scenarios in Relay Control System, in Proceedings of the 18th IFAC World Congress, pp. 13287–13292, Milano, 2011.
[CI8]

C. Bruschi, F. Della Rossa e F. Dercole, Consequences of technological innovation on stock quality and persistence, in Proceedings of the 7th European Nonlinear Dynamics Conference, ENOC2011, pp. 24–29, Roma, 2011.
[CI7]

S. Cerutti, G. Baselli, A.M. Bianchi, E. Caiani, D. Contini, R. Cubeddu, F. Dercole, L. Di Rienzo, D. Liberati, L. Mainardi, P. Ravazzani, S. Rinaldi, M. G. Signorini e A. Torricelli, Biomedical signal and image processing, in BioMed@POLIMI Proceedings of the 1st Workshop on the Life Sciences, pp. 319–333, Politecnico di Milano, 2010.
[CI6]

F. Dercole, C. Piccardi, S. Rinaldi e M. G. Signorini, Life and Bifurcations, in BioMed@POLIMI Proceedings of the 1st Workshop on the Life Sciences, pp. 356–360, Politecnico di Milano, 2010.
[CI5]

F. Dercole e C. Cecchetto, A new stock market model with adaptive rational equilibrium dynamics, in Proceedings of the 1st IEEE Conference on Complexity in Engineering, COMPENG 2010, pp. 129–131, Roma, 2010.
[CI4]

A. Colombo e F. Dercole, Border collision of non-hyperbolic fixed points, in Proceedings of the 2nd IFAC meeting related to analysis and control of chaotic systems, CHAOS 09, pp. 98–103, Londra, 2009.
[CI3]

A. Lazaric, E. Munoz de Cote, F. Dercole e M. Restelli, Bifurcation Analysis of Reinforcement Learning Agents, in Adaptive and Learning Agents and Multi-Agent Systems, K. Tuyls, S. de Jong, M. Ponsen, and K. Verbeeck (eds.), pp. 111–125, MICC Technical Report Series, Maastricht, Olanda, 2007.
[CI2]

F. Dercole e Yu. A. Kuznetsov, Boundary-value problems for sliding solutions continuation, in Proceedings NSA-UPRH Regional Conference on Global Continuation Methods in Three Dimensional Elasticity, Puerto Rico University Press, Humacao, PR, 2003.
[CI1]

F. Dercole, A. Gragnani e S. Rinaldi, Sliding bifurcations in relay control systems: An application to natural resources management, in Proceedings 15th IFAC World Congress, pp. 185–190, Barcellona, 2002.

Altre pubblicazioni

Editoriali

[ED1]

F. Dercole e S. Geritz Editorial, Journal of Biological Dynamics, 5, 103, 2011.
Rapporti interni

[RI4]

F. Dercole, U. Dieckmann, M. Obersteiner e S. Rinaldi, Adaptive dynamics and technological change, IIASA Interim Report IR-06-070, International Institute for Applied Systems Analysis, Laxenburg, Austria, 2006.
[RI3]

F. Dercole e Yu. A. Kuznetsov, SlideCont: An Auto97 driver for sliding bifurcation analysis, Preprint n. 1261, Department of Mathematics, Utrecht University, The Netherlands, 2002.
[RI2]

F. Dercole, Sliding bifurcations in relay control systems: An application to natural resources management, Internal Report n. 2002.16, Dipartimento di Elettronica e Informazione, Politecnico di Milano, 2002.
[RI1]

F. Dercole, Computation of the visible portion of a digital terrain, Internal Report n. 2001.81, Dipartimento di Elettronica e Informazione, Politecnico di Milano, 2001.

Pubblicazioni didattiche

[PD1]

F. Dercole, C. Piccardi e S. Rinaldi, Fondamenti di automatica: I parte Testo on-line per corsi da 5 e 10 crediti, ftp.elet.polimi.it/outgoing/Fabio.Dercole/fda/testo.pdf, 2001.

Software scientifico

[SS3]

E. J. Doedel, A. R. Champneys, F. Dercole, T. F. Fairgrieve, Yu. A. Kuznetsov, B. Oldeman, R. C. Paffenroth, B. Sandstede, X. J. Wang e C. H. Zhang, AUTO-07p: Continuation and bifurcation software for ordinary differential equations. Department of Computer Science, Concordia University, Montreal, QC, 2007.

[SS2]

F. Dercole, User Guide to BPCONT, Dipartimento di Elettronica e Informazione, Politecnico di Milano, ftp.elet.polimi.it/outgoing/Fabio.Dercole/bpcont/bpcont.tar.gz, 2007.
[SS1]

F. Dercole e Yu. A. Kuznetsov, User Guide to SLIDECONT Department of Mathematics, Utrecht University, The Netherlands, www.math.uu.nl/people/kuznet/cm/slidecont.pdf, 2003.

Tesi

[TH2]

F. Dercole, Evolutionary Dynamics through Bifurcation Analysis: Methods and Applications. Tesi di dottorato, Dipartimento di Elettronica e Informazione, Politecnico di Milano, 2002.
[TH1]

F. Dercole, Un'Interpretazione Modellistica del Romanzo ``Jules et Jim''. Tesi di laurea, Politecnico di Milano, 1999.

Inizio pagina

Ultimo aggiornamento: 14/11/2012